Machine Learning Primer for Clinicians–Part 12
Alexander Scarlat, MD is a physician and data scientist, board-certified in anesthesiology with a degree in computer sciences. He has a keen interest in machine learning applications in healthcare. He welcomes feedback on this series at drscarlat@gmail.com.

Previous articles:
- An Introduction to Machine Learning
- Supervised Learning
- Unsupervised Learning
- How to Properly Feed Data to a ML Model
- How Does a Machine Actually Learn?
- Artificial Neural Networks Exposed
- Controlling the Machine Learning Process
- Predict Hospital Mortality
- Predict Length of Stay
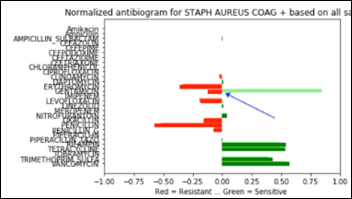
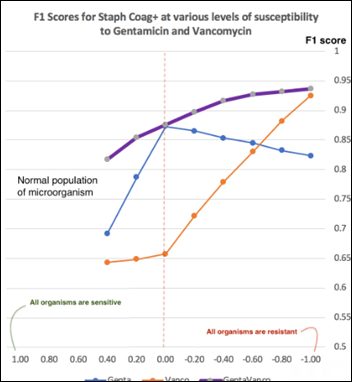
- Unsupervised Anomaly Detection in Antibiograms
- Basics of Computer Vision
Identify Melanoma in Images
In this last article in the “ML Primer for Clinicians” series, we’ll train a ML model to diagnose melanoma in dermoscopic images.The original data is the HAM10k images dataset, Human Against Machine with 10,000 Training Images, which is freely available.
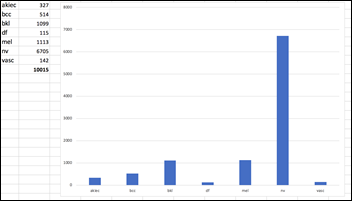
The dermoscopic images in the HAM10k dataset have been curated and normalized in terms of luminosity, colors, resolution, etc. The actual diagnosis was validated by histopathology (a.k.a. source of truth) in more than 50 percent of the cases, which is twice more than the previously available skin lesion datasets. The rest of the lesions’ diagnosis was based on a consensus of dermatologists. The 10k images in this dataset belong to the following seven diagnostic categories:
Actinic Keratoses – 327 images solar keratoses, intraepithelial carcinoma, Bowen’s disease (akiec)
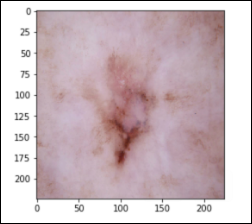
Basal Cell Carcinoma – 514 images (bcc)
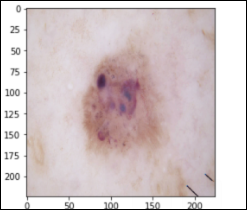
Benign Keratosis – 1,099 images seborrheic keratoses, senile wart, solar lentigo, lichen-planus like keratosis (bkl)
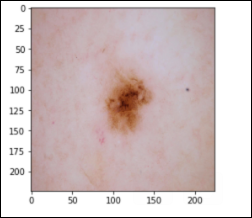
Dermatofibroma – 115 images (df)
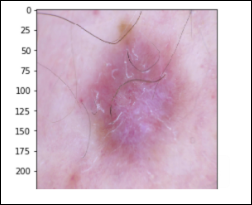
Melanocytic Nevus – 6,705 images (nv)
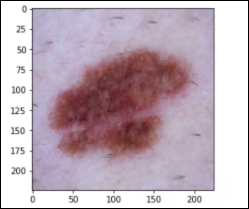
Melanoma – 1,113 images (mel)
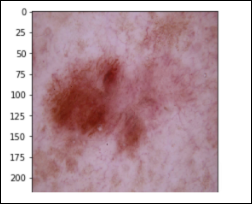
Vascular Lesions – 142 images cherry angiomas, angiokeratomas, and pyogenic granulomas (vasc)
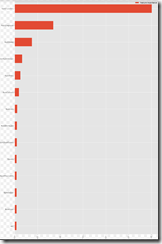
The dataset is imbalanced, as the number of images in each class varies from 115 (dermatofibroma) to 6,705 (nevus):
Instead of trying to classify seven skin lesions with a highly imbalanced dataset, let’s simplify the task to the diagnosis of Melanoma vs. Not Melanoma. If we summarize the above categories into two groups, the result is still an imbalanced dataset with:
- 1,113 Melanoma images
- 8,902 Not Melanoma
We can apply data augmentation to the Melanoma group and bring the number of images to be similar to the Not Melanoma group. Data augmentation applies a random combination of image modifications — such as zoom, angle, shift, horizontal and vertical flips, etc. — and creates synthetic images.
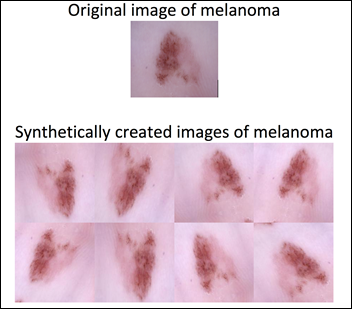
Data augmentation allows the model to be exposed to various modifications of an image of melanoma. This in turn allows the model to learn and later generalize, for example, that a melanoma pointing to the left is still a melanoma if it points to the right. The previously imbalanced 10k images become a 17.8k balanced dataset after the data augmentation of the melanoma group:
- 8,903 Melanoma images
- 8,902 Not Melanoma images
With such a balanced dataset, the guessing accuracy should be 50 percent. This is the baseline sanity check before we measure a machine performance on this binary classification task.
Melanoma or Not Melanoma
- Task: categorize a dermoscopic image as Melanoma or Not melanoma, a supervised binary classification challenge
- Experience: the 17.8k dermoscopic images dataset detailed above
- Performance: accuracy, precision, recall, F1 score, and ROC AUC
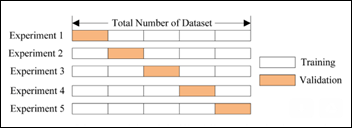
The newly created 17.8k images dataset is randomly split into three datasets:
- Train 10,682 images (60 percent)
- Validate 3,562 (20 percent)
- Test 3,561 (20 percent)
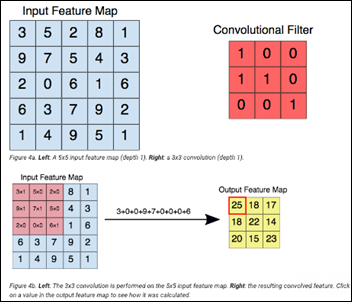
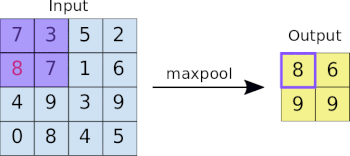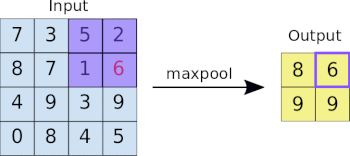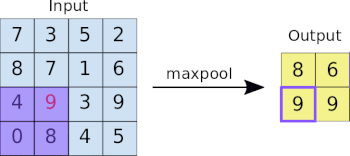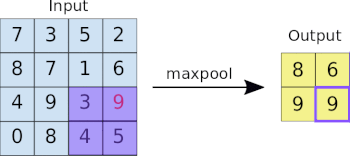
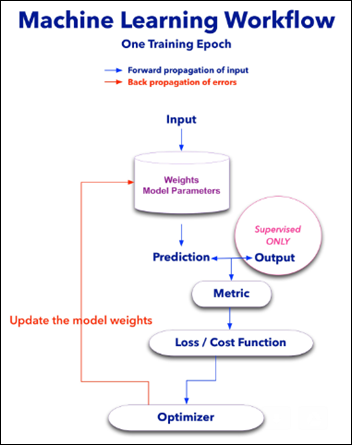
This image analysis challenge is approached from three angles, as explained in the last article:
- Create a convolutional NN (convnet) from scratch
- Use existing pre-trained models for feature extraction
- Fine tune existing pre-trained models
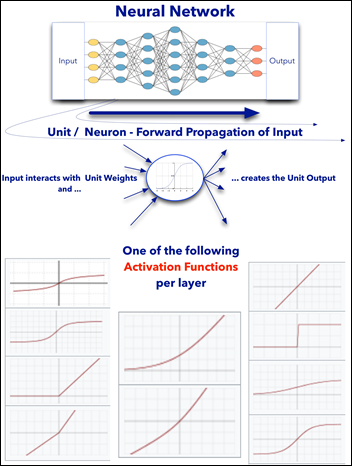
Common to all the following convolutional NN models:
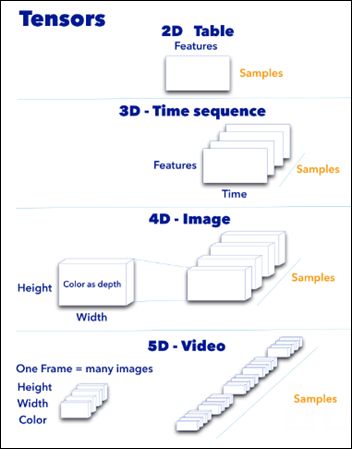
- Input layer that accepts an image as a tensor: image height (pixels) x width x color (RGB). The models tested accept images from 224x224x3 to 331x331x3.
- Output layer that predicts a probability between 0 and 1 for the image being Melanoma vs. Not Melanoma. The decision cutoff point is 0.5.
- In between the above two layers, various architectures of convolutional, pooling, dense, and normalization layers, with millions of trainable parameters (a.k.a. neurons)
Simple Convolutional NN
The Python code and the dataset for this part are publicly available.
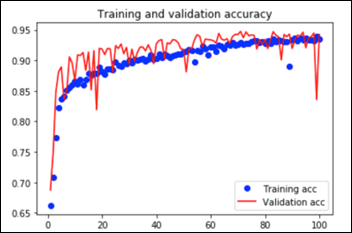
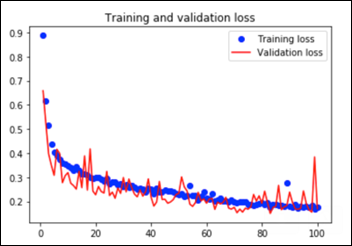
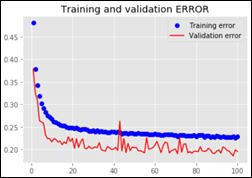
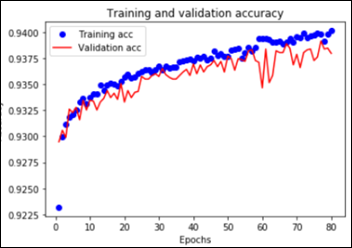
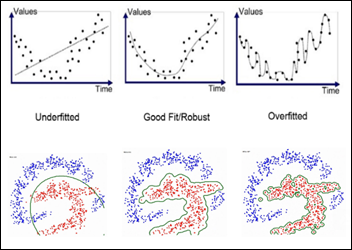
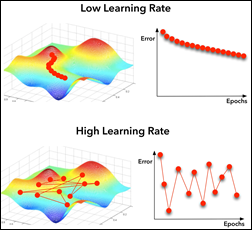
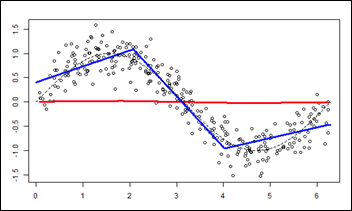
This convnet, with 9.7M trainable parameters, achieves an accuracy of 93 percent on the test dataset of images the model has never seen. The learning curves for 100 training epochs of this model, while using dropout, regularizers, and batch normalization techniques:
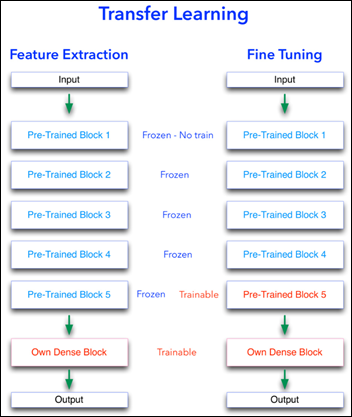
Transfer Learning
Feature extraction and fine-tuning are two common methods of transfer learning. For the following transfer learning, I’ve cross-validated eight open source, pre-trained image analysis models: VGG16, VGG19, ResNet50, InceptionResNetV2, Xception, InceptionV3, DenseNet201, and NasNetLarge. All these computer vision models are freely available as part of Keras, the ML framework used for this image analysis project.
Feature Extraction
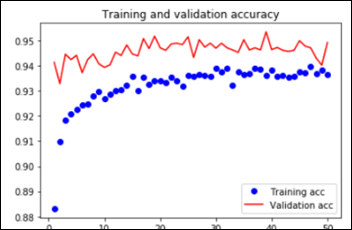
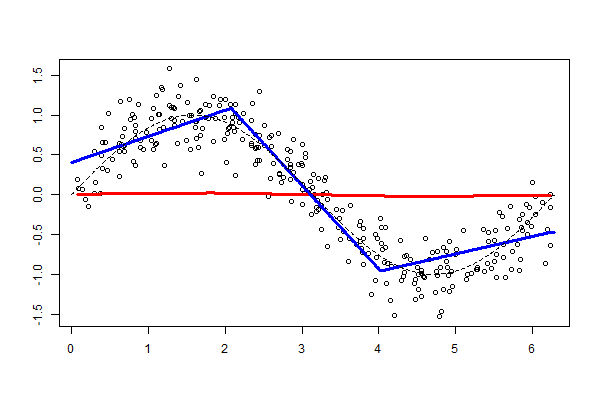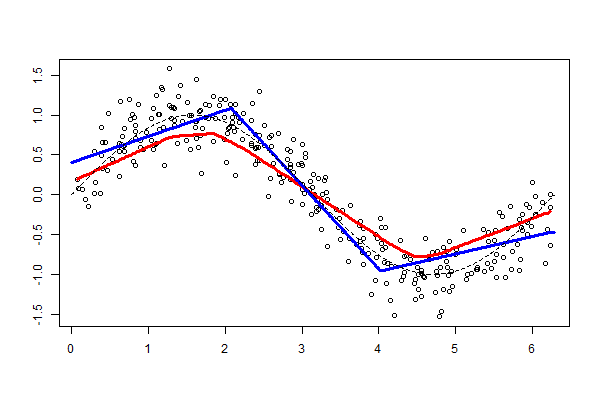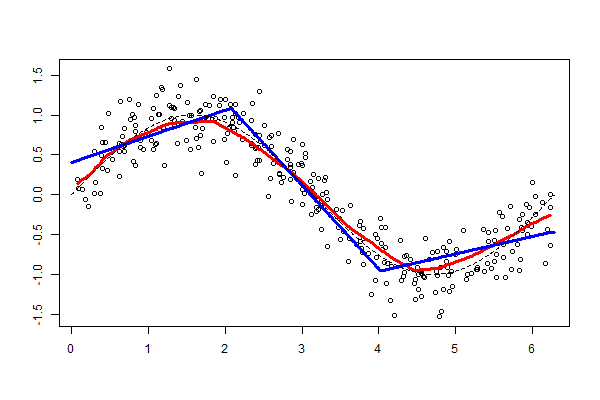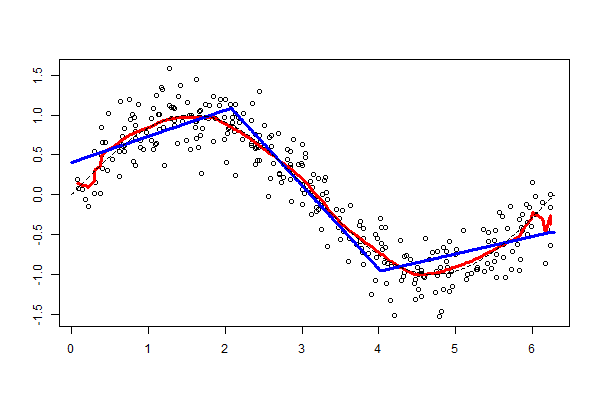
As explained in the last article, with feature extraction, we import one of the above models and freeze it so it won’t be modified during the training process and we add our own trainable layers on top of this pre-trained model. The lowest accuracy results: 86.3 percent with feature extraction on top of VGG16. The highest accuracy was achieved with a model extracting features from ResNet50, 94.5 percent. Note that after 50 epochs, this model was still underfitting on accuracy while perfectly fitting the loss function:
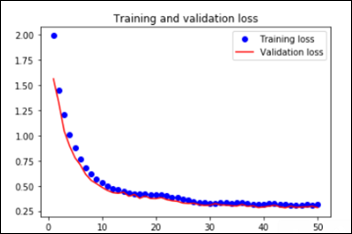
The Python notebook and the data for the feature extraction (ResNet50) are available.
Fine Tuning
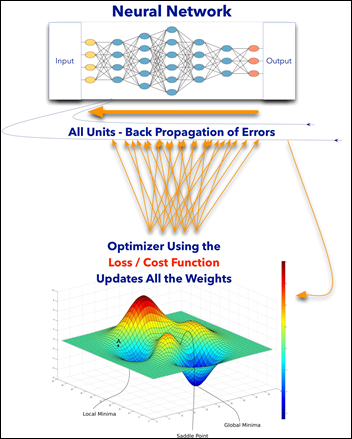
Fine tuning is slightly different that feature extraction. While we still import a pre-trained model and freeze it, we unfreeze the model last block of layers so these block weights will be modified during training. Fine tuning is usually done with a slow learning rate since we do not want to modify the pre-learned weights of the model last block too abruptly, as this may destroy the units (a.k.a. neurons) pre-learned “knowledge.”
The worst performance with fine tuning a pre-trained model was 92 percent – NasNetLarge. The best overall performance on this dataset – 94.7 percent accuracy – was achieved by fine tuning ResNet50, the same pre-trained model introduced above. This time the model has 10.8M trainable parameters and it displays the following learning curves:

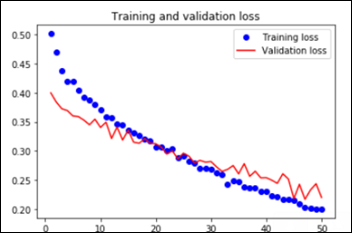
The Python notebook and the images dataset are available.
Model Performance Evaluation
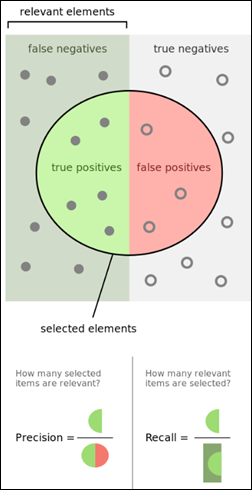
As previously mentioned, there are other metrics besides accuracy that convey information on the relevance of the results:
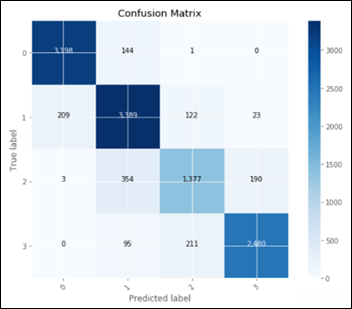
- Confusion matrix (TP,TN, FP and FN)
- Precision
- Recall
- F1 score
- ROC AUC
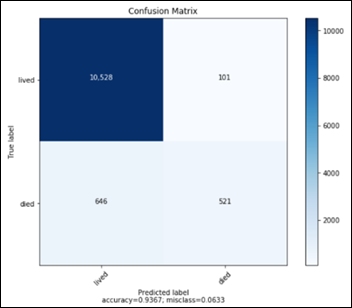
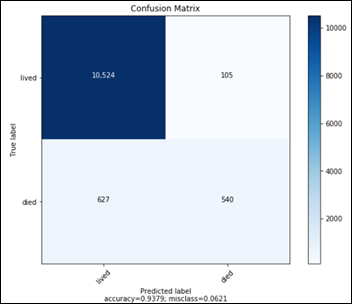
Considering only the best model in terms of accuracy, fine tuning on top of a pre-trained ResNet50:
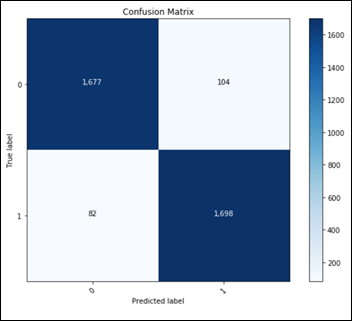
This confusion matrix translates into:
- TN: 1677
- FP: 104
- FN: 82
- TP: 1698
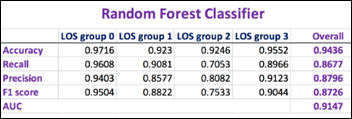
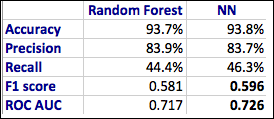
Final metrics for the best ML model:
- Accuracy: 94.8 percent
- Recall: 95.4 percent
- Precision: 94.2 percent
- F1Score: 0.948
- ROC AUC: 0.947
Performance Comparison on Similar Melanoma Identification Tasks
- Dermatologist ROC AUC performance varies between 0.69 and 0.91.
- Other ML models ROC AUC performance varies between 0.72 and 0.94.
Conclusions
- Using freely available infrastructure, framework, Python libraries, and a single dataset, one can build a ML model that outperforms both dermatologists and other ML models in the detection of melanoma in dermoscopic images.
- By definition, a learning algorithm will improve its performance on a specific task with each and every new experience learned, so the above algorithm is expected to improve beyond 94.8 percent accuracy if it will be exposed to additional relevant images.
- A fully operational ML model would have to predict in real time each new image it sees, whether it is melanoma or not, with the probability of the decision. Such a ML model will need to fine tune itself, on a daily or weekly basis, by being re-trained on newly labeled images, those with the ground truth reached by consensus or histopathology results. The periodical retraining of the ML model is analogous to the continued medical education of any healthcare professional.
- A reportedly shortage of dermatologists in the US, combined with the introduction of full-body 3D photography that produces hundreds and thousands of images per patient, may hint towards the future of this type of ML models — not replacing dermatologists, but supporting them with the pre-screening process of the millions of images coming their way.
Epilogue
I hope that the “ML Primer for Clinicians” series has clarified the main terms and concepts in AI, demystified some buzzwords, and in the process, has left you with some wisdom and curiosity about ML. My intention is to use this series of articles as the backbone of my third book, so please feel free to contact me with any issues, concerns, requests to modify, etc. related to this future manuscript. As I am always curious about new ideas in AI/ML in healthcare, please let me know about your interesting ML challenges.
Many thanks to Mr. HIStalk, who was kind enough to offer me a podium for my musing during the last couple of months. Without his initial spark, this “ML Primer for Clinicians” would not exist.



















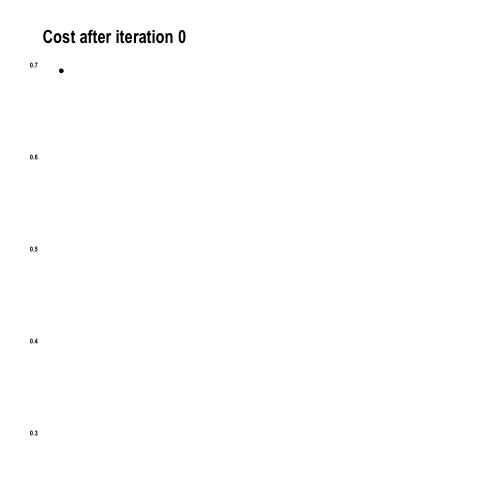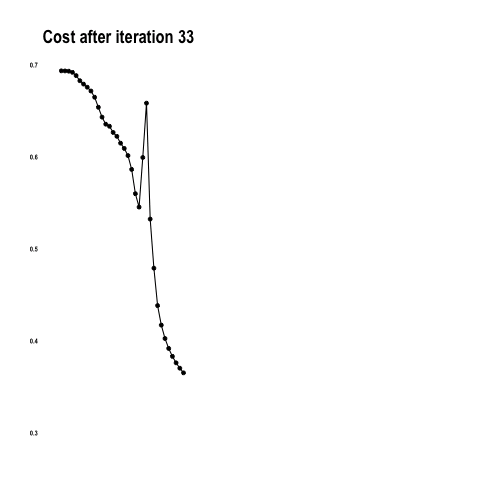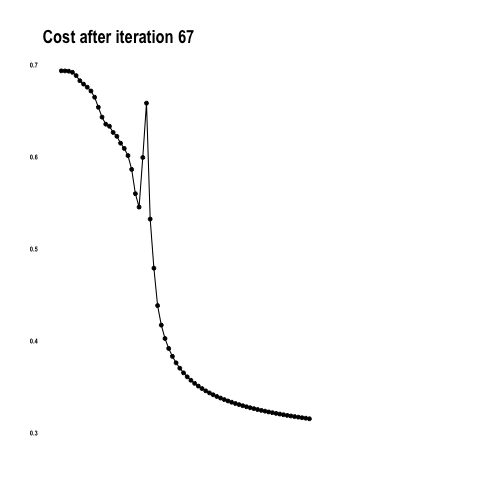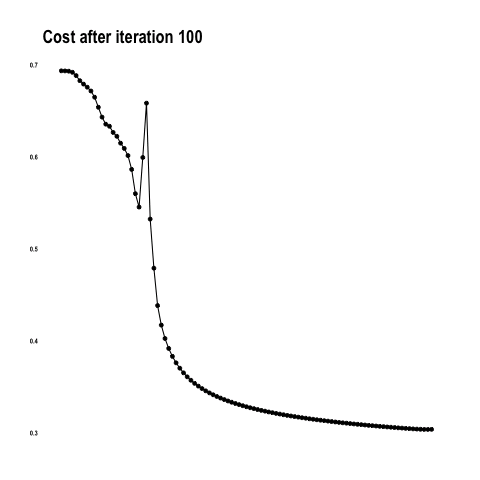








I've figured it out. At first I was confused but now all is clear. You see, we ARE running the…