A Machine Learning Primer for Clinicians–Part 6
Alexander Scarlat, MD is a physician and data scientist, board-certified in anesthesiology with a degree in computer sciences. He has a keen interest in machine learning applications in healthcare. He welcomes feedback on this series at drscarlat@gmail.com.

Previous articles:
- An Introduction to Machine Learning
- Supervised Learning
- Unsupervised Learning
- How to Properly Feed Data to a ML Model
- How Does a Machine Actually Learn?
Artificial Neural Networks Exposed
Before detailing what is a NN, let’s define what it is not.
As there is much popular debate around the question whether a NN is mimicking or simulating the human brain, I’ll quote Francois Chollet, one of the luminaries in the AI field. It may help you separate at this early stage between science fiction and real science and forget any myths or preconceptions you may have had about NN:
Nowadays the name neural network exists purely for historical reasons—it’s an extremely misleading name because they’re neither neural nor networks. In particular, neural networks have hardly anything to do with the brain. A more appropriate name would have been layered representations learning or hierarchical representations learning, or maybe even deep differentiable models or chained geometric transforms, to emphasize the fact that continuous geometric space manipulation is at their core. NN are chains of differentiable, parameterized geometric functions, trained with gradient descent.” (From “Deep Learning with Python” by Francois Chollet)
You’ve met already an artificial neural network (NN) in the last article. It predicted the LOS based on age and BMI, using a cost function and trained with gradient descent as part of its optimizer.
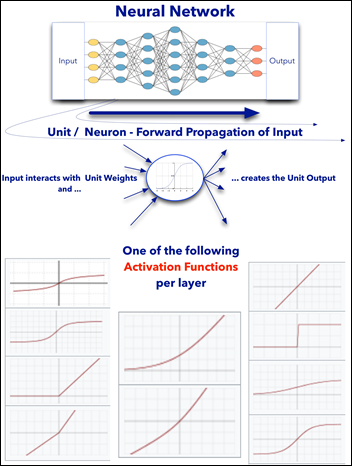
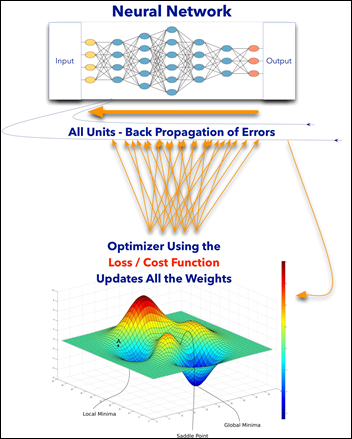
ANN Main Components
- A model has many layers: one input layer, one or more hidden layers, and one output layer.
- A layer has many units (aka neurons). Some ML models have hundreds of layers and tens of millions of units.
- Layers are interconnected in a specific architecture (dense, recurrent, convoluted, pooling, etc.)
- The output of one layer is the input of the next layer.
- Each layer has an activation function that applies to all its units (not to be confused with the loss / cost function).
- Different layers may have different activation functions.
- Each unit has its own weight.
- The overall arrangement and values of the model weights comprise the model knowledge.
- Training is done in epochs. Each epoch deals with a batch of samples from input.
- Each epoch has two steps: forward propagation of input and back propagation of errors (see above diagrams).
- A metric is calculated as the difference between the model prediction and the true value if it is a supervised learning ML model.
- An optimizer algorithm will update the weights of the model using the loss / cost function.
- The optimizer helps the model navigate the hyperspace of possibilities while minimizing the loss function and searching for its global minimum.
- After model is trained and it makes a prediction, the model uses the final values of the weights learned.
In the following example, a ML model tries to predict the type of animal in an image as a supervised classification task.
- An input layer on the left side accepts as input the image tensors as many small numbers.
- Only one hidden layer (usually there are many layers). It is fully connected to both the input and the output layers.
- An output layer on the right that predicts an animal from an image. It has the same number of output units as the number of animal types we’d like to predict. The probabilities of all the predicted animals should sum up to one or 100 percent.
From giphy.
What Is the Difference Between a NN and a Non-NN ML Model?
Non NN Models:
- One set of weights for the whole model.
- Model has one function (e.g. linear regression).
- No control over model internal model architecture
- Usually do not have local minima in their loss function
- Limited hyperspace of possibilities and expressivity
NN Models:
- One to usually many layers, each layer with its own units and weights.
- Each layer has a function, not necessarily linear.
- Full control over model architecture.
- May have multiple minima as the loss function is more complex.
- Can represent a more complex hypothesis hyperspace.
Remember the clustering exercise from a previous article?

- Task: given the X and Y coordinate of a dot, predict the dot color.
- Input: X and Y coordinates.
- Output: color of dot.
- Performance: accuracy of prediction.
How would a NN model approach the above supervised learning problem ?
Note that no centroids are defined, nor the number of classes (two in the above case) are given.
The loss function that the model tries to optimize results from the accuracy metric defined: predicted vs. real values (blue or orange). Below there are five units (neurons) in the hidden layer and two units in the output layer (actually one unit to decide if yes / no blue for example, would suffice as the decision is binary, either blue or orange.)
The model is exposed to the input in batches. Each unit makes its own calculation and the result is a probability of blue or orange. After summarizing all the layers, the model predicts a dot color. If wrong, the weights are modified in one direction. If right, in the opposite direction (notice the neurons modifying their weights during training). Eventually, the model learns to predict the dot color by a given pair of X and Y (X1 and X2 in the animation below)

From “My First Weekend of Deep Learning at Floyd Hub.”
Advantages of a NN Over a Non-NN ML Model
- Having activation functions, most of them non-linear, increases the model capability to deal with more complex, non-linear problems.
- Chaining units in a NN is analogous to chaining functions and the result is a definitely more complex, composite model function.
- NN can represent more complex hypothesis hyperspace than non-NN model. NN is more expressive.
- NN offers full control over the architecture: number of layers, number of units in a layer, their activation functions, etc.
- The densely connected model introduced above is only one of the many NN architectures used.
- Deep learning, for example, uses other NN architectures: convoluted, recurrent, pooling, etc. (to be explained later in this series). Model may have a combination of several basic architectures (e.g. dense on top of a convoluted and pooling).
- Transfer learning. A trained NN model can be transferred with all its weights, architecture, etc. and used for other than the original intended purpose of the model.
The last point of transfer learning, which I’ll detail in future articles, is one of the most exciting developments in the field of AI. It allows a model to apply previously learned knowledge and skills (a.k.a. model weights and architecture) with only minor modifications to new situations. A model trained to identify animals, slightly modified, can be used to identify flowers.
Next Article
Controlling the Machine Learning Process



I've figured it out. At first I was confused but now all is clear. You see, we ARE running the…